Int-4 LLaMa is not enough - Int-3 and beyond.
More compression, easier to build apps on LLMs that run locally.
Last Thursday we demonstrated for the first time that GPT-3 level LLM inference is possible via Int4 quantized LLaMa models with our implementation using the awesome ggml C/C++ library. We were amazed by the overwhelming response from the community and the various tools they built. Most notable is the GitHub repo with 4.5k+ stars on a similar LLaMa Int4 implementation as us released by the creator of ggml himself. Some have even dubbed this as the stable diffusion movement for LLMs.
Today we share more exciting news about prospects of running LLMs locally on two fronts: Lowering the RAM utilization of these models through quantization beyond Int-4, and easier to build python apps using faster LLM inference
GPTQ-style quantization improves performance over naive Round-to-Nearest (RtN) baseline in nearly all cases, but it degrades for smaller model depending on the type of quantization performed.
The bin-size for Int4 quantization can be further increased from the current size of 32 without much performance degradation, leading to a 15% reduction in RAM required to store weights for even the 7B LLaMa model.
LLaMa 13B can be int3 quantized (with much larger bin size) with not much additional performance drops over int4 quantization, leading to a 30-35% reduction in RAM required to store weights for larger models.
While int2 quantization is not usable for LLaMa 13B, larger models may be 2-bit quantize-able without much performance drop.
Int3 & Int4 LLaMa Quantization.
Larger transformer models have long-since known to be more compression friendly. We adapt and study 7B and 13B LLaMa model GPTQ quantization over the two ggml quantization formats - fixed-zero offset and variable zero-offset quantization.
In k-bit quantization, the weight matrix are quantization to range {0, 1, … k-1} with a scaling factor and a zero-offset factor as follows:
Usually multiple consecutive `x_{fp16}` share `scale` and `zeroOffset` - this is currently hard coded to 32 consecutive elements (also known as ‘groups’ or ‘bins’) in the both the current implementations.
Experimentation:
All experiments assume fp16 format for `scale` and `offset`. Both the current C/CPP LLaMa implementations over ggml uses fp32 - it should be doable to add fp16 support.
We follow GPTQ paper’s as closely as possible in our experiments:
We evaluated only on a subset of WikiText & PTB-256 samples of 2048 sequence.
Our calibration data was 128 sequence of 2048 tokens, all from WikiText dataset.
We fixed the percent dampening (λ) to 0.01.
1. Variable zeroOffset quantization
Here both the `zeroOffset` and `scale` factor are separately stored. In both the current LLaMa int-4 C++ implementations, this is GGML_TYPE_Q4_1 type. This gives better quality output than having a fixed `zeroOffset`, at the cost of extra storage.
Note: Most demos/implementations we have seen consider the other quantization type (fixed zeroOffset quantization).
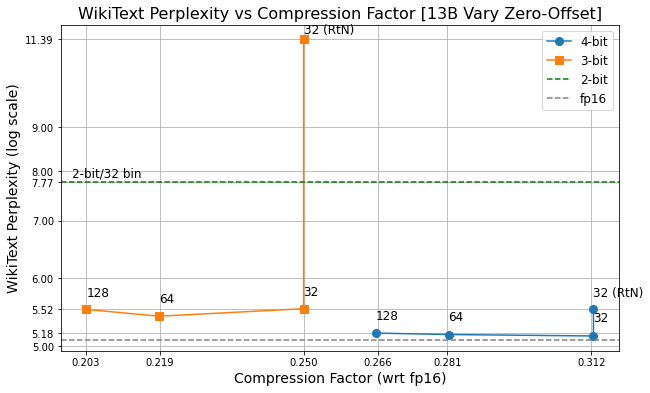
13B LLaMa (32, 64, 128 are the bin sizes; RtN is baseline). Currently 4-bit (RtN) with 32 bin-size is supported by GGML implementations.
We notice very little performance drop when 13B is int3 quantized for both datasets considered.
While Rounding-to-Nearest (RtN) gives us decent int4, one cannot achieve int3 quantization using it. GPTQ clearly outperforms here.
int2 is still far from reach with the GPTQ method on both the dataset.
7B LLaMa (32, 64, 128 are the bin sizes; RtN is baseline). Currently 4-bit (RtN) with 32 bin-size is supported by GGML implementations.
We observe a similar pattern at 13B, except the performance degradation from int3 is much more significant for 7B, compared to int4.
2. Fixed zeroOffset quantization
This is the quantization approach where the zero-offset (zeroOffset) is fixed to 2^{k-1} for a k-bit quantization. In both the current LLaMa int-4 C++ implementations, this is type. Only the `scale` parameter needs to be stored for each bin. In both the current LLaMa int-4 C++ implementations, this is GGML_TYPE_Q4_0 type.
13B LLaMa (32, 64, 128 are the bin sizes; RtN is baseline). Currently 4-bit (RtN) with 32 bin-size is supported by GGML implementations.
Observations over 13B are same as when using variable zero-offset quantization.
7B LLaMa (32, 64, 128 are the bin sizes; (32 RtN) is baseline). Currently 4-bit (RtN) with 32 bin-size is supported by GGML implementations.
7B with fixed zeroOffset is an interesting outlier for 4-bit quantization, where GPTQ gives much worse results than RtN baseline. We tested with multiple seeds, but got similar results. Our hypothesis is that this could be due to certain outlier groups/bins, for which the fixed zero-offset serves as a terrible offset during quantization - this remains to be tested.
PyLLaMa
We are currently developing a Python wrapper for the gglm.cpp codebase with the aim of making it more accessible to a wider range of developers. Our primary goal is to simplify the usage of the gglm.cpp library and make it more user-friendly. In addition to this, we plan to implement server hosting functionality similar to Cocktailpeanut's Dalai Lama, which will further enhance the library's accessibility and usability for developers. Our ultimate objective is to enable developers to easily incorporate the capabilities of gglm.cpp into their projects and facilitate its use for a broader range of applications.
Furthermore, we intend to integrate support for Google's Flan series and GPT-Neo, both of which are truly open-source language models. By incorporating these additional models into our offering, we aim to create a comprehensive and versatile toolkit that can be used for various applications. Our overarching goal is to provide developers with a flexible and powerful toolkit that can be utilized to tackle a wide range of challenges and problems.
Coming Soon (within this week)
Int3-quant C/C++ Kernels using ggml and LLaMa runtime benchmark on Macbook with Neon Intrinsics.
Get a green-light from Meta to release the Delta of quantization weights. To maximize the possibility of this happening, please share this blog.
Explore SparseGPT prospects of compression - (More than 25% of connections in 13B LLaMa are zeroed out when int3 quantized!)
CodeGen 6B, GPT-J 6B & Pythia 6.9B fast-inference via PyLLaMa.
Resources
GPTQ-for-LLaMa - We used this implementation for experiments.
Welcomed Contributions
We evaluated only on a subset of WikiText & PTB-256 samples of 2048 sequence length, following GPTQ. We encourage contributing perplexity scores on GPTQ with larger validation sets.
We encourage people to contribute experiments with more number of sequences than 128 sequence from diverse domains (for example Pile’s GitHub & StackExchange, SODA, Instruct datasets like P3).
We did not tune the percentage dampening (λ) hyperparameter from default 0.01 used throughout GPTQ paper. This is another area which needs to be explored.
2-bit quantization for LLaMa 33B and 65B seems promising given relative performance of 2-bit 13B over 7B. This is another potential useful compression waiting to be explored. It is also easier to write fast kernels for 2-bit than 3-bit.









What's the status here? Did it get resolved seems like U ruffled lots of feathers on HN
But what's the status?
The post mentions future work, but this was 3 months ago, and I don't see anything updated. Even on github.